3 : 132人目の素数さん : ~~~終了~~~ 4 : 132人目の素数さん : 1307 リーマン予想>ポアンカレ予想幾何学I 演習問題No6 略解 問題 58 f − 1 が連続であることを言えば良い.このためには X の閉集合 F に対して f ( F ) が Y の 閉集合であることを示せばよい.幾何学II 演習問題No1 19年10月2日 問題1 3単体jabcdjの境界の定める単体複体K = K(@jabcdj) を考える.チェイン 複体C (K)の(向き付けられた) 単体からなる基底をとり,境界作用素@ Cp(K)!

中古 7160 問題解法 幾何学辞典 第2版 笹部貞市郎 聖文社 平成元年 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版
英語 幾何学問題
英語 幾何学問題-多様体は高次元の図形の概念として もっとも確立しているものである. 多様体の概念は,大学3年以後での幾何学の一番の基礎であるだけではなく, 現代数学の多くが多様体上で行われるという意味で, 現代数学全体の基礎でもある. 授業計画と内容幾何学辞典 問題解法 著者 長沢亀之助 撰著 出版者 長沢亀之助 出版年月日 明治40 シリーズ名 数学辞典叢書 請求記号 特2736 書誌id(国立国会図書館オンラインへのリンク) doi / 公開範囲 インターネット公開(保護期間満了) iiif マニフェストuri




初等幾何学 Youtube
幾何学A 問題 第1 回 1(宿題) 球面S 2に立体射影により局所座標系を入れて,U0 = S ∖{(0,0,1)},U1 = S2 ∖{(0,0,−1)}, φ0 (x,y,z) → (X0,Y0) = x 1−z y 1−z ,φ1 (x,y,z) → (X1,Y1) = x 1z y 1z とする. (1) 座標変換φ1 φ−1 0 を計算せよ. (2) Z0 = X0 iY0,Z1 = X1 −iY1 とした場合にZ1 をZ0 で表せ.数学 難易度総合ランキング 2 : 132人目の素数さん : 2ゲットズサ━━━━⊂ (゚Д゚⊂⌒`つ≡≡≡━━━━!!Z0 z1 7!z1=z0 を考える。C 上でz = xiy と表わしたときに、その上の二次微分形 式を!
1 位相幾何学の問題 問題11 整係数のホモロジー群は同型になるが、同相にはならないような位相空間の例を挙げよ。 問題12 オイラー数は等しくなるが、ホモロジー群は同型にならないような位相空間のNov 02, 14 · 1 高校数学幾何学の問題 ΔABCがあり,AC=BC=1, ∠ACB= 휋 2 である.点Pは線分 BC上を動き,点Qは∠APQ= 휋 2 をみたすようにして線分AB上 を動く.このとき,線分AQの 長さの最小値を求めよ. A B P C Q 1 1 2 次のスライド以降では3通りの解法を述べたい と思う. 解法を見る前に一度自分で考えてみよう. 3S1 をr(x) = x=jxjで定義すると、変形レ トラク になる ことを示せ。
三角形の内角の和は180°? 「三角形の内角の和」は必ず180°。 でも、それは"ユークリッド幾何学の世界"での話です。 三角形がふつうの平面じゃなくて、ボールの表面のような「球面」に描かれていたら、どうでしょう? 内角の合計は180°より大きくなるはずです。 極端に言えば「三つの角が全部90°」なんていう三角形だって描けてしまうでしょう。 球面上の幾何学 (きかがく、 古代ギリシア語 γεωμετρία )は、 図形 や 空間 の性質について 研究 する 数学 の分野である 。 もともと測量の必要上からエジプトで生まれたものだが、人間に認識できる図形に関する様々な性質を研究する数学の分野としてとくに 古代ギリシャ にて独自に発達し 、これらのおもな成果は紀元前300年ごろ ユークリッド によって問題72 (07年度幾何学I試験問題) CP1 の非同次座標' U0 = fz0 z1 j z0 6= 0 g !



四訂版対応 体系問題集 数学2 幾何編 中学2 3年生用 基礎 発展 学参ドットコム 通販 Yahoo ショッピング




問題解法 幾何学辞典 笹部貞市郎 聖文社 第二版 大学受験 絶版参考書 博物館
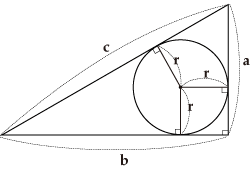
9 代数学の質問です(偶置換と奇 10 代数学の問題で困っています。 11 y=x^(1/x) の 微分;Q9 図のような3辺の長さがa,b,cの直角三角形の内接円の半径rを求めなさい。 ヒント 三角形の面積と内接円の関係を使って考えてください。 解答はこちら Q10 図のように直線上で接する二つの円があるとき、直線との接点間の距離を求める公式は容術で幾何学I 演習問題No1 (年4月15日) 第1回レポート課題 以下の問題2を解いて,4月21日1700までにPandAでオン ラインで提出してください. 今回のレポート課題はオンラインでの提出の練習,および,PC環境等が整って




ベクトルの問題を解きました 計算は特になにも問題はなかったんですが 最後の幾何的意味 Clear




彫刻されたアンティーク数学的および幾何学的問題彫刻アンティークイラスト1851年発行 19世紀のベクターアート素材や画像を多数ご用意 Istock
幾何 (中 1 ) 《 平面図形 》 1 章01 平面図形の基礎1 問題 1 章02 平面図形の基礎2 問題 1 章03 対称な図形 問題 1 章04 図形の移動 問題 1 章05 作図1 問題幾何学II演習問題 担当 中島啓 08年10月15日(水) 問題8 授業で省略した Hk c (M) ˇ ˝ e Hk1 c (M R) が互いに逆写像になることの証明を与えよ。 問題9 (1) 写像r R2 nf0g !射影幾何学はいわば, この私たちの目に見える世界をそのままの形で幾何学の世界 に移したものであります。注意として,平行な2直線の無限の彼方には,同じ無限遠点 があると考えます。例えば真っ直ぐ延びる線路の上に立っていることをイメージする




とある初等幾何の超難問の解法



1
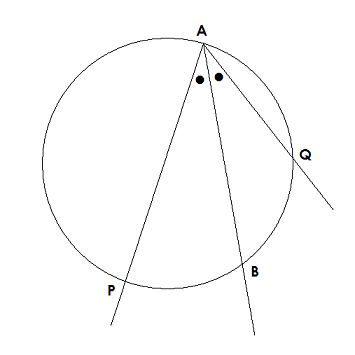
Cr幾何学の諸問題 (複素幾何学の諸問題) 平地, 健吾 (1103) 数理解析研究所講究録, 1731 fano多様体の諸問題 (複素幾何学の諸問題) 高木, 寛通 (1103) 数理解析研究所講究録, 1731数論幾何 ~幾何学的な直感で問題解く~ 未来発見フォーラム14 東京国際フォーラム 慶應義塾大学理工学部 坂内健一Nov 04, · 数学 幾何学1の問題です。 2130 定理54「2点ADが直線BCの同じ側にあって、角BDC=角BACならば四点A,B,C,Dは同一円周上にある。 」の証明の中で点Dが円Yの外側にある場合に弦BC上の点Mを持ち出さなければならないそうなのですが、なぜ点Mを持ち出さ
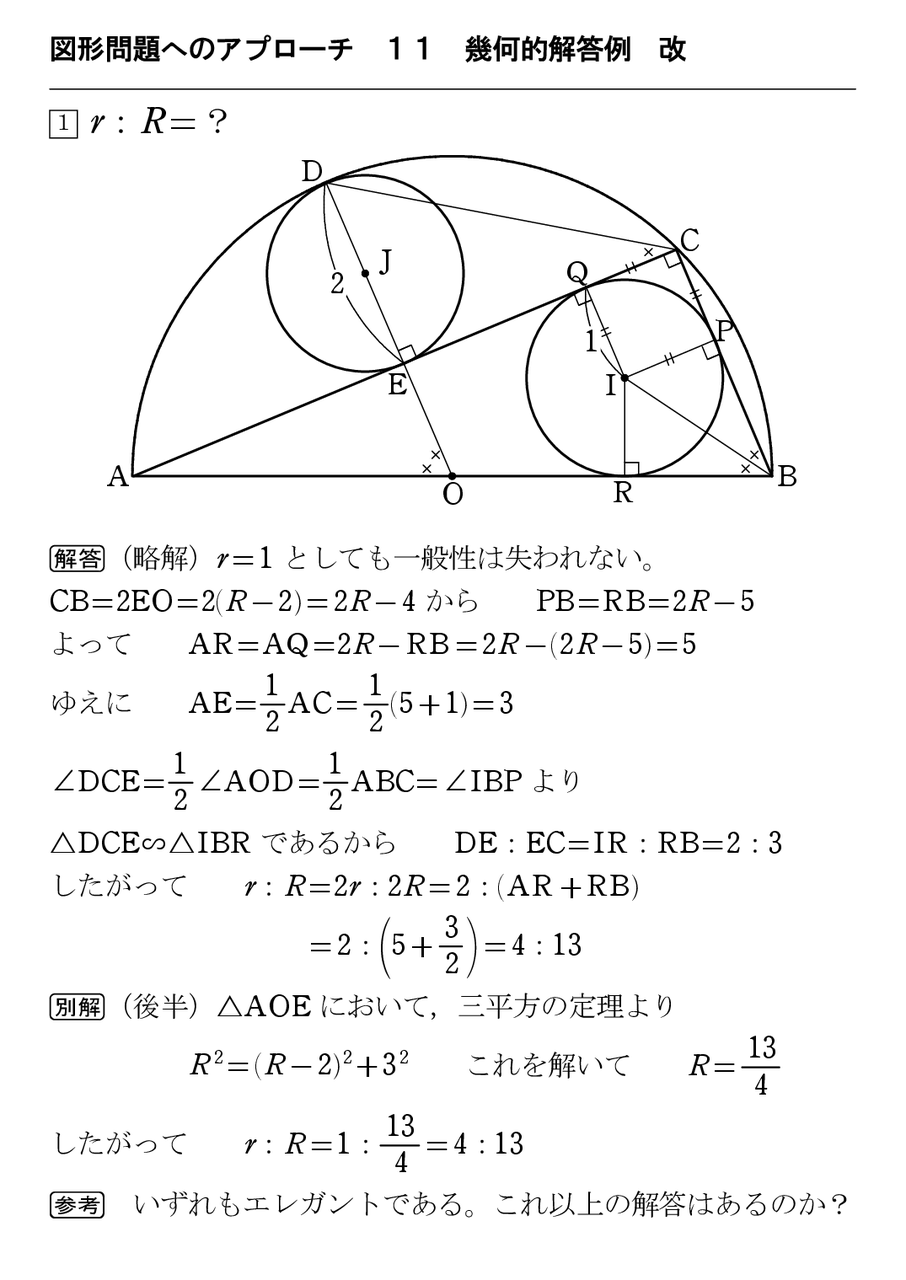



平面幾何 怜悧玲瓏 高校数学を天空から俯瞰する




明倫館書店 やさしい幾何学問題ゼミナール
中学入試でよく出題される,あるいは差がつく問題ばかり100題を集めました。 がんばる受験生に役立つことを願って作成しています。 1ページ(の大きさ)に4題ずつ。 切り分ければハガキ大の大きさになって,電車の中でもファミレスでお料理が来る前にでも,いつでもどこでも学習することができます。 問題1~問題4 問題5~問題8 問題9~問題12 問題13~問題1 特殊関数の問題 パンルヴェ性をめぐって (複素幾何学の諸問題) 1 北海道大学理学院 岩崎 克則 (Iwasaki,Katsunori) 2 調和解析の問題から (複素幾何学の諸問題) 14 九州大学大学院数理学研究院 野村 隆昭 (NOMURA,Takaaki) 315 代数学の質問です準同型写像の 16 数学の集合で閉じているの意味 17 数学の微分です;
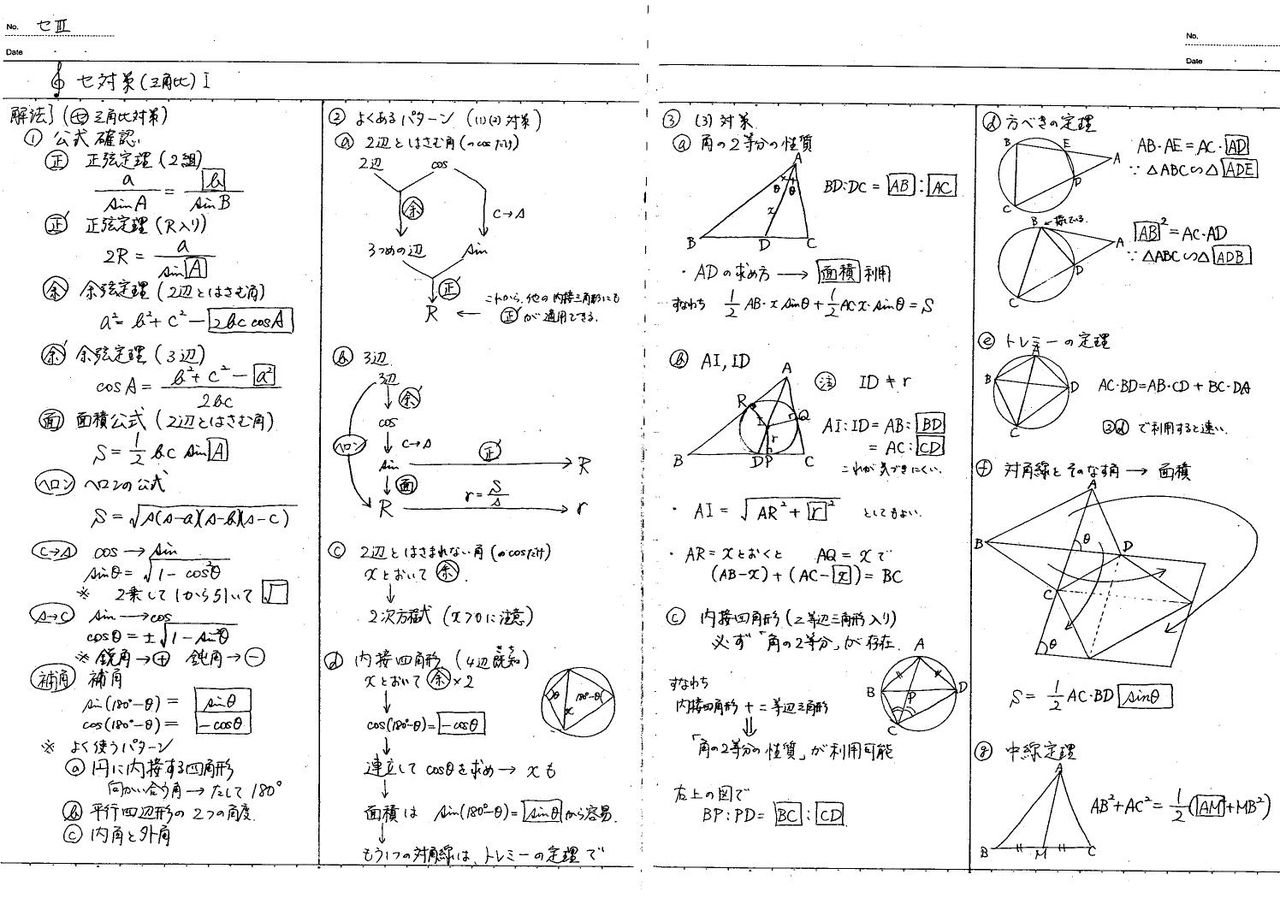



図形問題へのアプローチ 3 怜悧玲瓏 高校数学を天空から俯瞰する




警視庁受験 伊藤塾 警視庁過去問解説第一弾 1類図形判断 幾何学 問題 1問は補助線と相似関係に気が付けば4分以 Facebook
18年度 1q 幾何学特別講義a (zuab331) 東京工業大学理学院数学系; 18年5月8日 幾何学特論a (mthb401) 東京工業大学理学院数学系数学コース; 18年5月8日 微分積分学第一・演習 (lasm101);18年6月7日 (定期試験問題と解答例) 東京工業大学理工系教養科目Apr 19, · 概要 計算幾何学はコンピュータグラフィックスの発展、計算機支援のデザインや操作 (cad/cam) の研究分野としての側面を主な動機として展開されたが、計算幾何学における問題は、その多くが自然界における古典的な幾何学の問題である。 ほかに、計算幾何学の重要な応用は次のものが芥川 和雄 (中央大) 幾何解析の問題 平地 健吾 (東大) cr幾何, 共形幾何の問題 9月8日 (水) 午前 河澄 響矢 (東大) リーマン面に関連する位相幾何学の問題 宮地 秀樹 (金沢大) タイヒミュラー空間論の問題 午後 望月 拓郎 (京大数理研) 一般化ホッジ理論の問題




補助円を使う証明問題 中学3年生の数学より 身勝手な主張




よく理解できる数学講座 初等幾何学の問題 一辺が 15cm の正方形abcd の辺ad の中点をf Facebook
演習問題解答シリーズ 著作権等への考え方については数学書の演習問題の解答集を参照。 演習問題解答:Engelking「General Topology」問題62 f をS1 上のC1 級関数とし、問題48のようにdxを取って、S1 上の1次微分形 式α = f(x)dx を考える。このときα = dg となるようなS1 上のC1 級関数g が存在する ための必要十分条件は、 ∫ S1 α = ∫1 0 f(x)dx = 0 であることを証明せよ。オイラーによる「ケーニヒスベルクの 7 つの橋」問題の解決は位相幾何学の萌芽(のひとつ)であるとみなされている。 ユークリッド幾何学 が紀元前にはできていたことと比較すると、 オイラー や ガウス に始まる位相幾何学は高々 250 年の歴史であり、大きな差がある。



平面幾何問題 Of 京極一樹の数学塾会員頁




三角形と円の幾何学 数学オリンピック幾何問題完全攻略の通販 安藤 哲哉 紙の本 Honto本の通販ストア
幾何学I 演習問題No3 略解 問題 26 Cb をいつものように二つの座標近傍 ( U 1 ;φ 1 ), ( U 2 ;φ 2 ) で覆う.すなわち, U 1 = C, φ 1 ( z ) = z および U 2 = C f1g , φ 2 ( z ) = 1モンジュの問題 次のような問題を考えます。 問題1:ある砂山をそれと同じ体積の穴に移したい。 砂粒の移動には移動距離に依存したコスト がかかるとき、最適な移動のさせ方は何 か? この問題は仏の数学者・工学者である Gaspard曲線と曲面の幾何学・演習問題—No2— 線形代数の準備1(続き) 問A15 2b ac>0 とする。曲線ax2 2bxy cy2 = 1 が、漸近線のなす小さい方の 角が π 3 であるような双曲線となるための、a,b,cに関する必要十分条件を求めよ。 問A16 λ6= 0 ,β6= 0 とする。λX2 βY = 0 で与えられる全ての放物線は



平面幾何問題 Of 京極一樹の数学塾会員頁



幾何学大辞典 1 基本定理と問題 平面 岩田至康編 明倫館書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋
幾何学概論第二定期試験〔問題1〕 注意事項 解答は, 解答用紙の所定の欄に, 採点者が読みとり, 理解できるように書いてください 計算や下書きには余白・裏面を使用してください(採点の対象ではなNov 02, · 明星大学通信教育部 過去問 「幾何学 2 PF40」 (問題) 頂角Aが °の二等辺三角形 ABC において,辺 AB,AC 上に点 D,E をそれぞれ∠ BCD=60 °,∠ CBE=50 °となるようにとる。 このとき,∠ DEB は何度か。 (解説) 教科書 32 ページにこの問題「3.3 先生方を悩ます難問」が載っています。 「頂角Aが °の二等辺三角形 ABC において,辺 AB,AC 上に点 D,E をそれぞれ∠Dec 11, 17 · この記事は 数学とコンピュータⅡ Advent Calendar 11日目の記事です。 こんにちは、佐野です。12月といえば Advent Calendar の季節です🎄思いつきで 数学とコンピュータ Advent Calendar Ⅰ / Ⅱ を立ち上げたところ、嬉しいことに二つともすぐに満員となりました。エントリーして下さった




高校数学 幾何学の問題 やや難




数学 幾何学1の問題です 定理5 4 2点adが直線bcの同じ側にあっ Okwave
計算幾何学の代表的問題(2) 点位置決定問題 平面上に直線で描かれた平面地図が与えられているとき, 質問点を含む領域の名前を求めよ. 質問点の付近だけを探索する ことによって,質問点を含む 領域の名前を求めることが できるか? 平面地図のすべて= dx^dy (1x2 y2)2 によって定義する。 (1)!Oct 06, · 8 幾何学の質問②;




高校数学i a 幾何学編 数学b 数学 各種問題集の通販 By なおちゃん S Shop ラクマ




書籍紹介 初等幾何学 清宮俊雄 著 数学
高校上級生から大学生,数学教師などを対象とした,初等的な幾何学問題集(解答付)。 考える練習や論理の展開の訓練に好適。 やさしい幾何学問題ゼミナール / ピーター・フランクル 前原 濶 著 共立Cp 1(K)の行列表示を求めよ.また(整数係数の)ホモロジーHp(K) を計算せよ.た だしa;b;c;d 2 R3 は一般の位置にある何学的に解釈し なぜ アルゴリズムがうまく働くかについて直観的イメージを与 える ' 統計的推定の幾何学的なイメージ ここではまず 与えられたデータに対して確率モデルをあてはめるという一般的な 問題に対して幾何学的な意味づけを与える ' まず
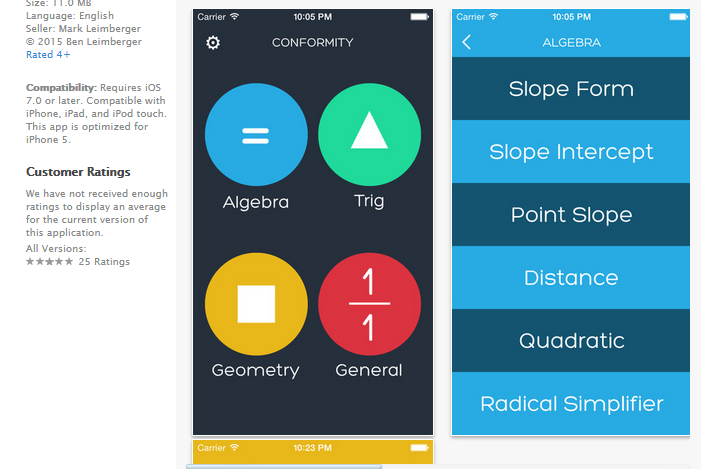



幾何学や三角法問題も簡単に解けるアプリ 15歳の高校生が開発 アイデアニュース




初等幾何学 Youtube
52 ユークリッド (幾何学に王道なし) 直線を最短距離を与える線と定義すれば, 球面上に三角形を描くと内角の和が180 度を超える たとえば, 地球上では, 経度0 度線, 経度90 度線, 赤道の3 つの直線によって三角形を描くことが でるが, この三角形はすべての角が直角になるJun 08, 18 · 数論幾何(ちゃんと言うなら数論幾何学)は数学の中の一分野で、 整数に関する様々な問題を幾何学的な手法を使って研究する学問 です。 のことで、0とそれに1ずつ足していって得られる数と1ずつ引いていって得られる数全体の集合のことです。 このOct 01, 19 · 本書は山辺の問題の解決の全貌を描いたものである.幾何解析学において,山辺の問題は,正質量問題,山辺不変量などとも関連する広い射程が認められるが,証明の構造は入りくんでいる.本書はこの全貌を,基本的な議論から出発し,意を尽くした説明




幻語 bake 学者 幾何 図形問題に挑戦 10 Answer 2 Fg 算数 小学生 Maths Math Mathematics 図形 幾何 Mathematik Mathematiques Matematika 中学生 Matematika Matematica 幾何学 数学 Matematicas Geometry



面積 これが中学入試に出た図形問題
情報学 労働法 アクティブ・ラーニング 宇宙・天文 文化資源 外国語の講演 物理学 科学技術 HOME > 講義を探す > 非線形有限要素法特論 > 第7回 幾何学非線形問題の有限要素定式化2




高校数学 幾何学の問題 やや難




辞書 辞典 笹部貞市郎 解析幾何学辞典 問題解法 送料無料の通販はau Pay マーケット Hmv Books Online




とある初等幾何の超難問の解法




数列と幾何学 関西大学入試問題 総合マネジメント事務所エスパスミューズ
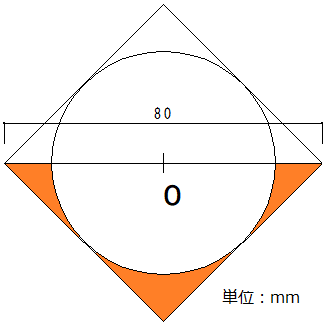



Cadで幾何学 Wawabubu なおぼん のblog




代数学と幾何学 円周率近似値の日に生まれて理系じゃないわけないだろ Knifeのblog
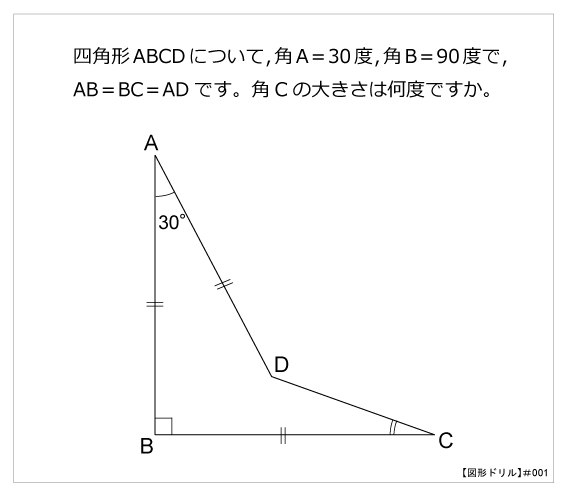



図形ドリル 算数星人のweb問題集 中学受験算数の問題に挑戦 図形ドリル 算数星人のweb問題集 中学受験算数の問題に挑戦




高校数学i a 幾何学編 数学b 数学 各種問題集の通販 By なおちゃん S Shop ラクマ




幾何学的変分問題の通販 西川 青季 紙の本 Honto本の通販ストア
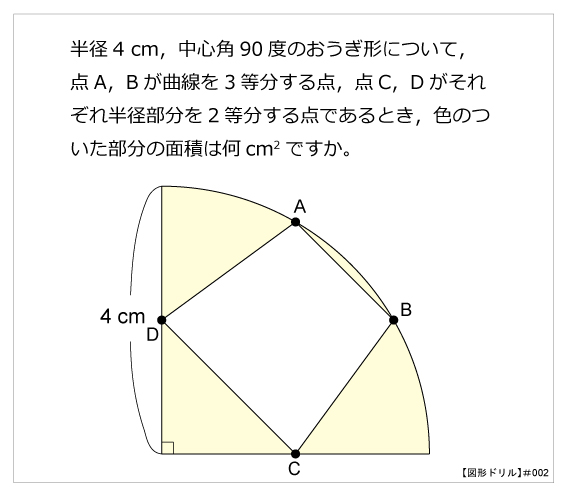



図形ドリル 算数星人のweb問題集 中学受験算数の問題に挑戦 図形ドリル 算数星人のweb問題集 中学受験算数の問題に挑戦
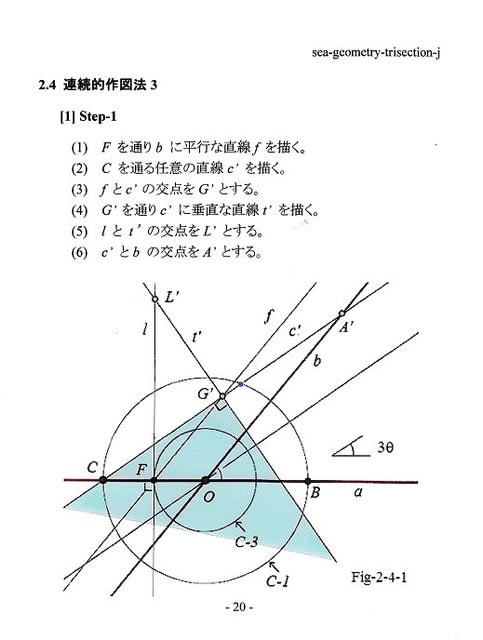



108 角の三等分の幾何学 の出版のお知らせ 6 8 角の三等分は可能である




中古 7160 問題解法 幾何学辞典 第2版 笹部貞市郎 聖文社 平成元年 の落札情報詳細 ヤフオク落札価格情報 オークフリー スマートフォン版



幾何学 Wikiwand




Pdf 和算の幾何学に現れたアルベロス 大鳥羽の問題
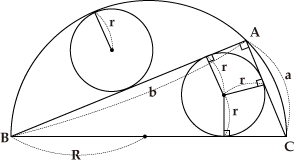



腕試し問題 幾何の問題 江戸の数学



幾何学的変分問題 岩波書店
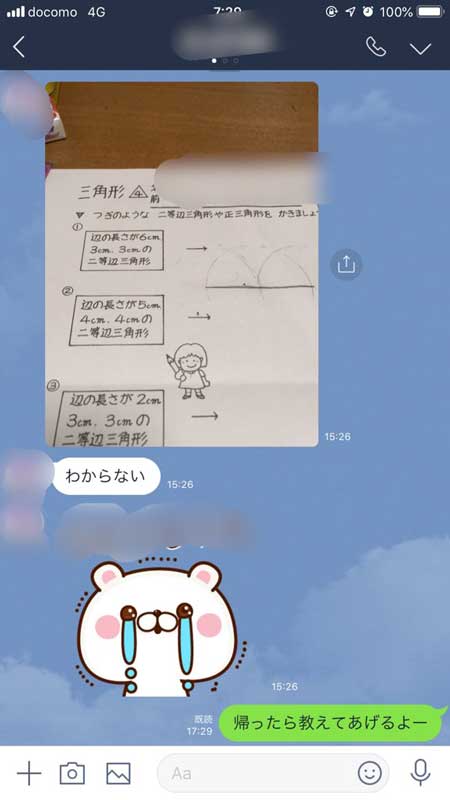



娘の算数の宿題が鬼畜難易度 これは難問 俺も解けない 非ユークリッド幾何学教えてるのか ねとらぼ



1




中学数学 図形編 新装版 パーフェクトコース問題集 学研プラス 本 通販 Amazon



初等幾何の詐欺 Langley S Problem



平面幾何 京極一樹の数学塾




1日10分 幾何学 問題集 Para Android Apk Baixar




ねこ騙し数学




問題解法 幾何学辞典 笹部貞市郎 聖文社 第二版 大学受験 絶版参考書 博物館
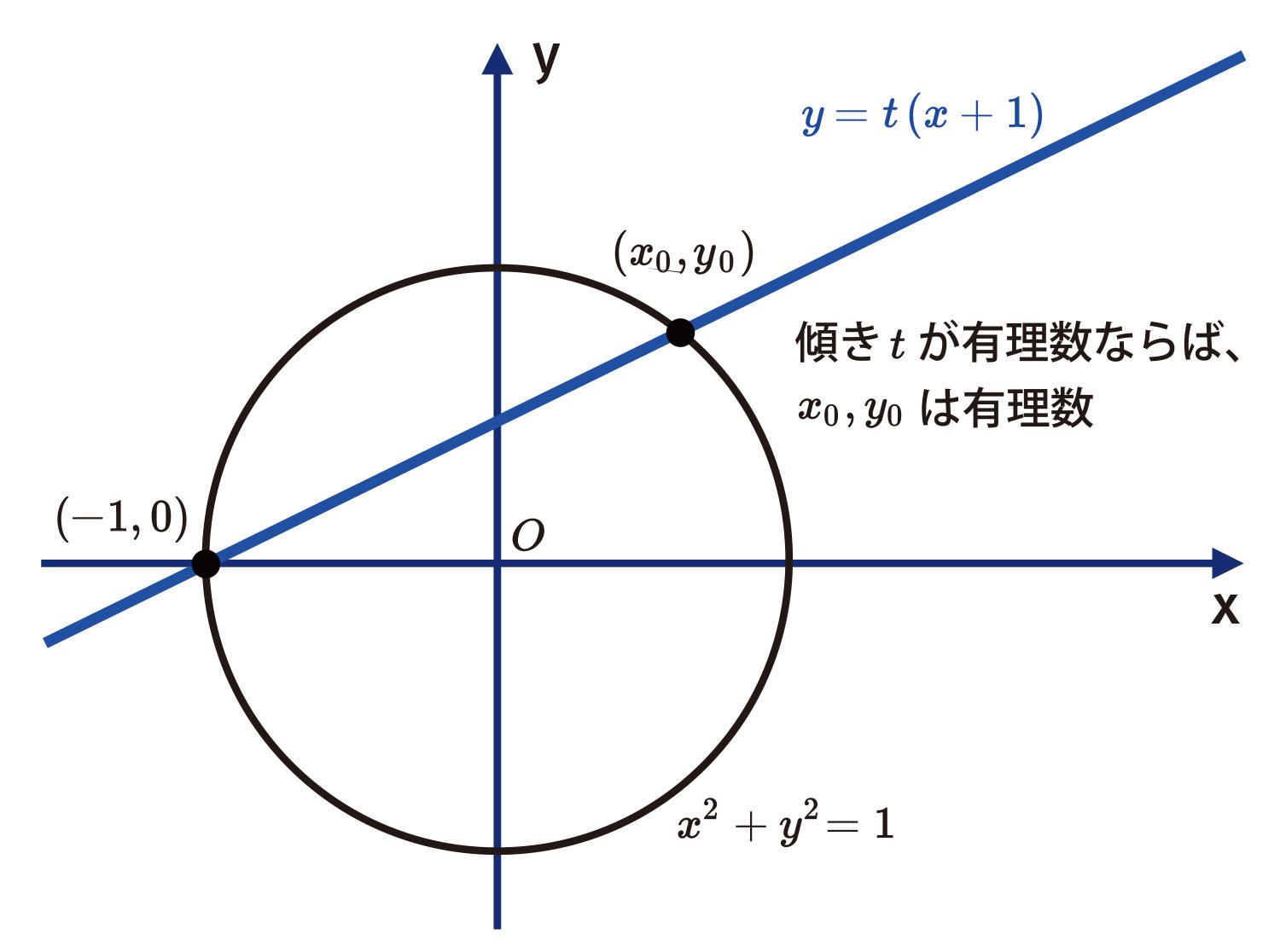



慶應理工の数論幾何 慶應義塾大学理工学部
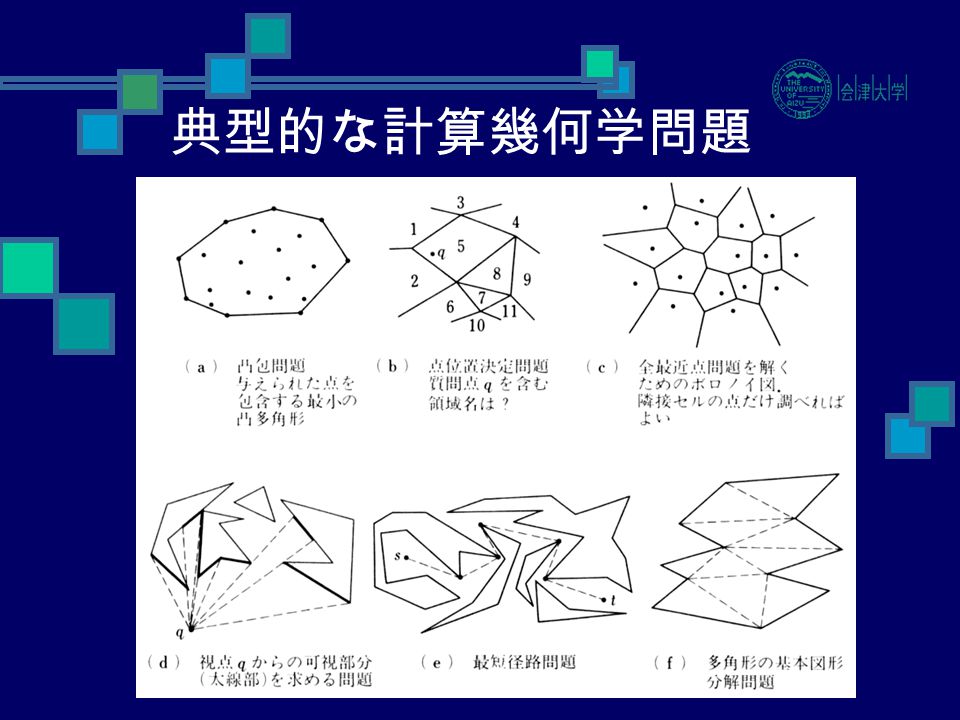



計算幾何学 Computational Geometry 第一章 基本概念 Basic Concepts Ppt Download
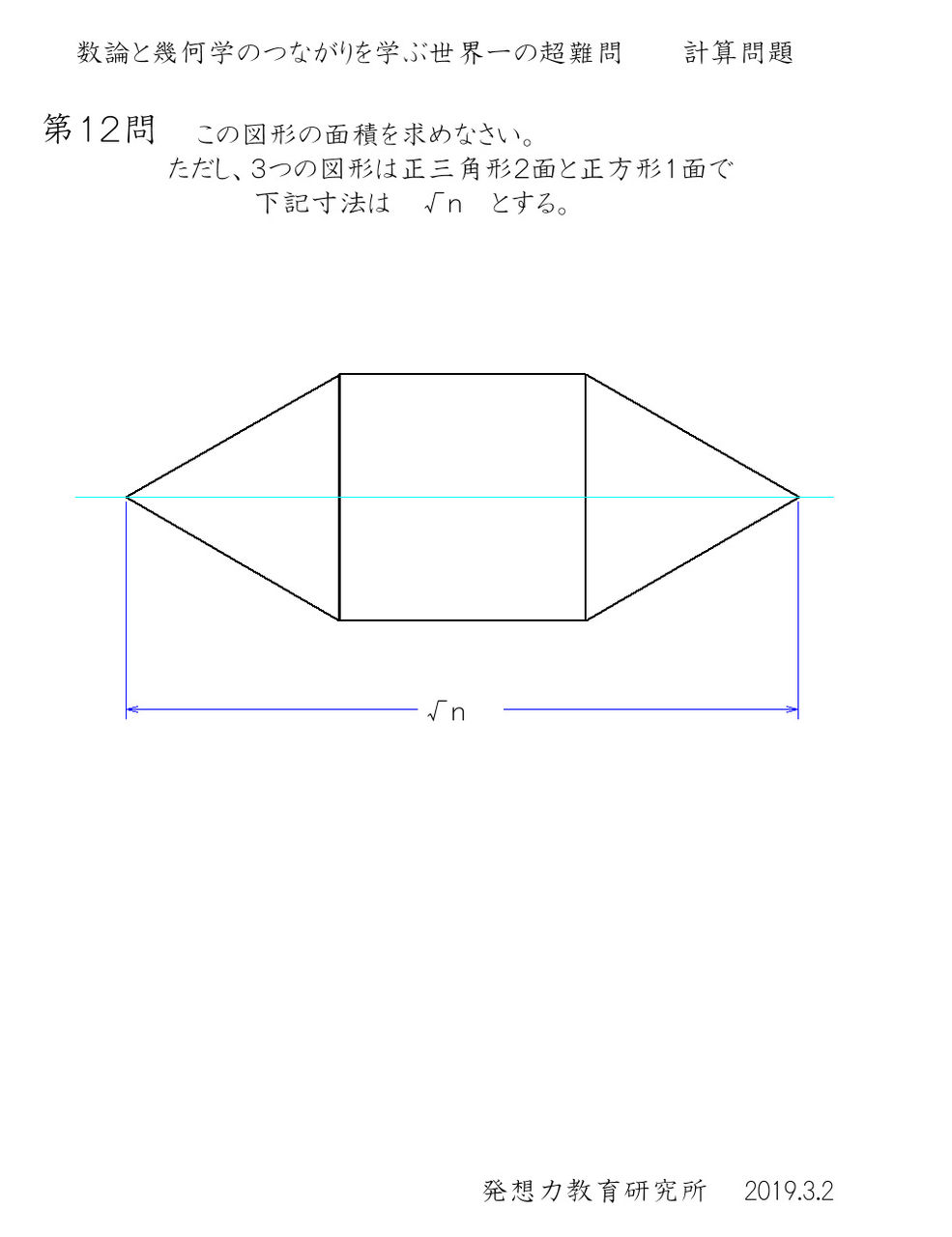



第12問 数論と幾何学の繋がりを学ぶ世界一の超難問 計算問題 第12 問 を出題しました 発想力教育研究所 素数誕生のメカニズム




古い幾何学辞典の問題1問 笹部貞市郎 問題解法 幾何学辞典 より 身勝手な主張



三角形と円の幾何学 安藤 哲哉 著 海鳴社 版元ドットコム
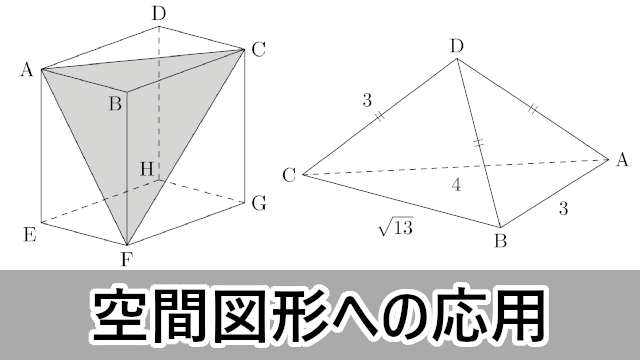



数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法



小学生の算数 図形 面積 体積 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 小学生
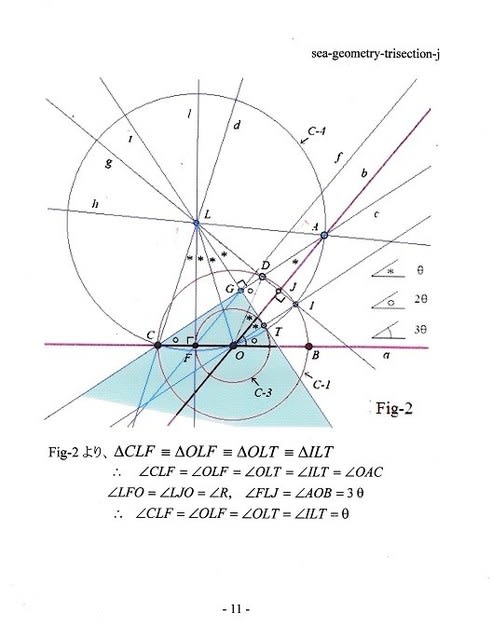



107 角の三等分の幾何学 の出版のお知らせ 5 8 角の三等分は可能である



すぐには解けない図形問題 Wrikk S Blog




幾何学の問題です 友達とやっているんですけど 本当に全くわからないです Clear




ラングレーの問題 Wikipedia




幾何学的変分問題 オンデマンド版の通販 西川 青季 紙の本 Honto本の通販ストア




図形問題 Twitter Search




Pdf 和算の幾何学に現れたアルベロス 渡辺の問題



1日10分 幾何学 問題集 Para Android Apk Baixar




Basic数学 19年7月号 大学入試問題演習 幾何学 オヨヨ書林



超絶難問 ラングレーの問題 時習館 ゼミナール 高等部




中学生でも解ける 図形問題 Hackmd



算額における幾何学




ひらめきに頼らず中学数学の図形問題を解く7つのコツ



1日10分 幾何学 問題集 Para Android Apk Baixar




黒い背景にロボット シルエットの木製のブロック異なる色で人間の幾何学的図形創造的論理的思考や問題解決の概念フラットが横たわっていた平面図ですコピー スペース おもちゃのストックフォトや画像を多数ご用意 Istock



E 教材 集合




大学入試 苦手対策 三角比 平面 空間図形 に強くなる問題集 旺文社




ジュニア算数オリンピック 二次元上のユークリッド幾何の問題 その16 ニート歴10年からの数学日記



平面幾何問題 Of 京極一樹の数学塾会員頁



腕試し問題 幾何の問題 江戸の数学




三角形と円の幾何学 数学オリンピック幾何問題完全攻略 哲哉 安藤 本 通販 Amazon




ヤフオク 岩波講座 現代数学の展開 非線形問題と複素幾何



非線形問題と複素幾何学 岩波書店




数学叢書第二十六編 初等 幾何学定量問題全 林鶴一 中島宗治 ロンサール書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




商品詳細 深遠なる 幾何学 の世界 創元社




メルカリ 体系問題集 数学2 幾何学 基礎 発展 参考書 300 中古や未使用のフリマ



平面幾何問題 Of 京極一樹の数学塾会員頁
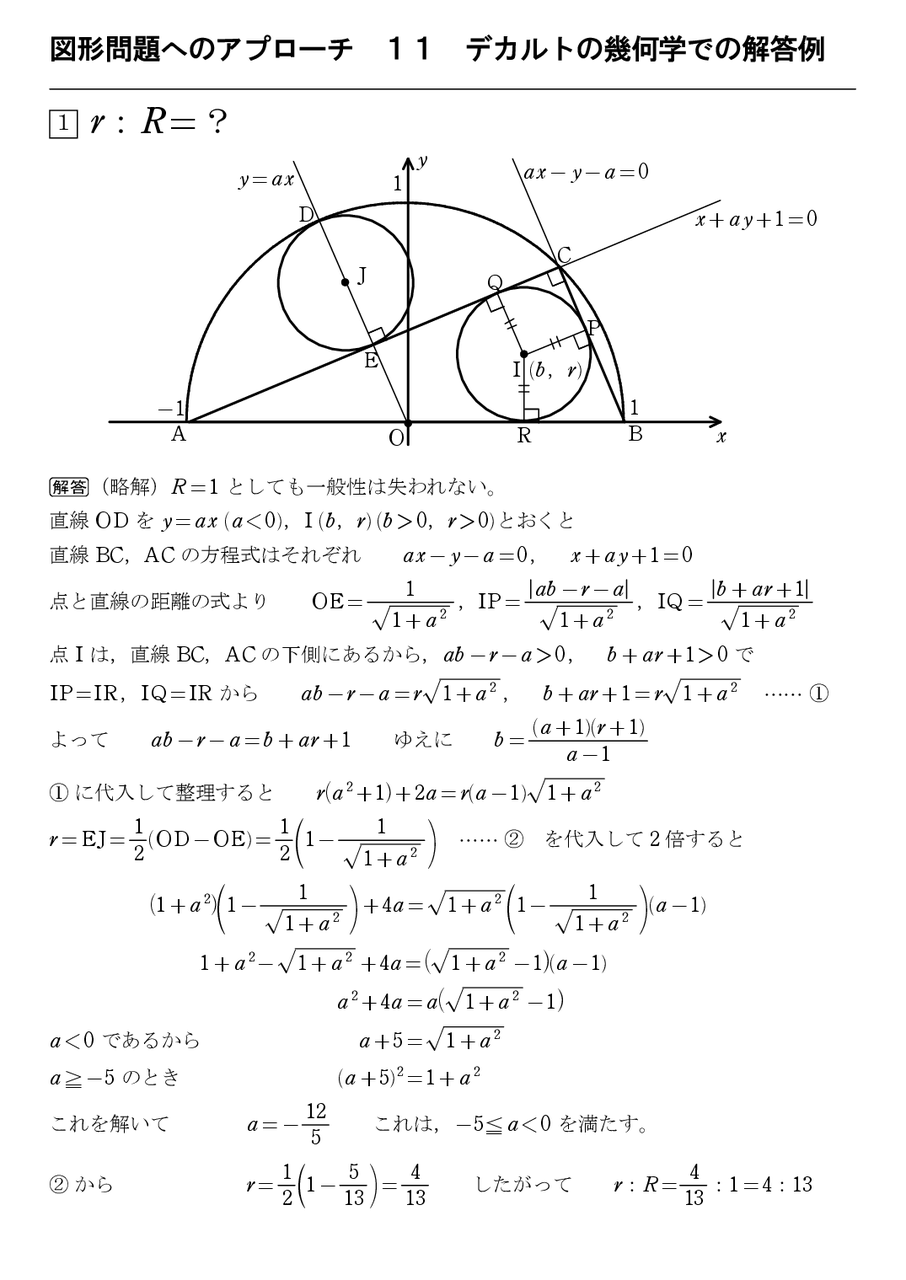



図形問題へのアプローチ 15 怜悧玲瓏 高校数学を天空から俯瞰する



幾何学的変分問題 岩波書店



1




幾何学問題の解き方 教材研究 笹部貞市郎 著 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




三角形と円の幾何学 数学オリンピック幾何問題完全攻略 哲哉 安藤 本 通販 Amazon




初等幾何学作図問題 窪田 忠彦 本 通販 Amazon




幾何学的関係ってなんですか 物理の問題文にあったんですが Clear




中学1年生 数学 平面図形の移動 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生



Q Tbn And9gcqswtbuzz0hhhpmkw0v Pfnkrbqviruafslod4gmpmz3cswyzf8 Usqp Cau



平面幾何 京極一樹の数学塾




高校数学 幾何学の問題 やや難




伝説の入試数学 図形問題 超シンプルなのに難問 Youtube



幾何学における未解決問題集 2 940円 数学侍 秋山仁先生の書籍サイト




新aクラス中学幾何問題集 5訂版 新aクラスシリーズ 市川 博規 本 通販 Amazon




主役は直角三角形 高校入試 数学の良問を解く




ベクトルの図形への応用を初等幾何学で解く 再び チェバ メネラウスの定理を使って 身勝手な主張
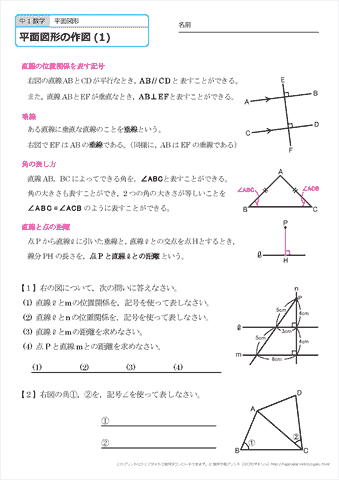



中学1年生 数学 平面図形の作図 練習プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




数学オリンピック 幾何の中古 未使用品を探そう メルカリ




新制 平面幾何学問題集 三省堂編輯所編 明倫館書店 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




平面幾何学の問題が解りません 幾何の問題 こどもの幾何 が解け 数学 教えて Goo




中学数学の中点連結定理を使う初等幾何学の問題を1問解こう 身勝手な主張




学生の幾何学辞典 問題解法 笹部貞市郎著 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋



0 件のコメント:
コメントを投稿